Kurz-Info: Archimedes – Das antike Jahrtausend-Genie

Der Begriff Genie wird häufig recht leichtfertig verwendet. Wenn es jedoch um Archimedes von Syrakus geht (ca. 287 – 212 v.Chr.), kann man diesen Begriff verwenden, ohne Angst haben zu müssen, damit der inflationären Verwendung dieses Begriffs weiteren Vorschub zu leisten.

Selbst das Prädikat Jahrtausend-Genie ist in seinem Fall durchaus angemessen. In puncto mathematisches Talent werden gemeinhin nur Newton und Gauss als ihm gleichwertig erachtet. Es wird vereinzelt sogar die Auffassung vertreten, dass es Newton und Gauss zur Ehre gereicht mit Archimedes in einem Atemzug genannt zu werden.

Aus moderner Sicht war Archimedes zugleich Ingenieur, Physiker und Mathematiker.

Seiner Ingenieurskunst zuzurechnen sind z.B.:

• Die Erfindung der Archimedischen Schraube – ein trickreiches Hilfsmittel zur Förderung von Flüssigkeiten, das noch heute vielfach zur Bewässerung von Feldern eingesetzt wird;

• Der Bau eines Planetariums;

• Die diversen von ihm ersonnenen Kriegsmaschinen mit denen Archimedes den Römern die Eroberung seiner Heimatstadt Syrakus im Zweiten Punischen Krieg deutlich erschwerte.

Als es den Römern 212 v.Chr. nach langer Belagerung (und wie berichtet wird, durch Verrat begünstigt) endlich gelang Syrakus zu erobern, kam Archimedes entweder dabei oder kurz danach ums Leben.

Einer berühmten, aber nicht unbedingt zutreffenden Legende zufolge, soll Archimedes in mathematische Studien vertieft, Figuren in den Sand gezeichnet haben, als – nach dem Fall von Syrakus – ein römischer Söldner an ihn herantrat. Dieser hatte den Auftrag das berühmte antike Genie zum römischen Befehlshaber Marcellus zu bringen. Archimedes wies den römischen Legionär mit den Worten „Zerstöre meine Kreise nicht“ (noli turbare circulos meos) zurecht. Daraufhin erschlug der verärgerte Legionär Archimedes.

Archimedes, der fast sein ganzes Leben in seiner Heimatstadt Syrakus verbrachte, hat in seinem schier unglaublich produktiven Leben bereits vor mehr als 2000 Jahren physikalische Gesetze gefunden, die bis heute gelehrt werden und nach wie vor zur Grundbildung in den mathematisierten Naturwissenschaften zählen:

• Archimedes hat das Prinzip des hydrostatischen Auftriebs (auch Archimedisches Prinzip genannt) gefunden

• Und das Hebelgesetz (unter besonderem Bezug zur Balkenwaage) in seiner bis heute gelehrten mathematischen Gestalt zu Papier gebracht. Es ist dieses Hebelgesetz, das hinter dem Archimedes zugeschriebenen Ausspruch „Gebt mir einen festen Punkt und ich hebe die Welt aus den Angeln“ steht.

Mit dem Hebelgesetz und dem damit aufs engste verbundenen Begriff des Schwerpunkts beginnt die Geschichte der mathematisierten Mechanik. Als nach der in vielerlei Hinsicht dunklen Zeit des europäischen Früh- und Hochmittelalters ab der Renaissance in Europa wieder Archimedes gelesen wird, entwickelt sich aus den von Archimedes geschaffenen Anfängen schnell unsere heutige klassische Mechanik. Man kann mit einiger Berechtigung die einschlägigen Arbeiten von Galilei wie Newton als durch die von Archimedes eingeführte Denkweise der mathematisierten Mechanik inspiriert einstufen.

Die für die westliche Wissenschafts- und Kulturgeschichte so prägende Entwicklung der mathematisierten Mechanik wurde also von Archimedes auf den Weg gebracht. Nicht das Geringste seiner vielzähligen Verdienste.

Zur Hydrostatik, einer weiteren Wissenschaft für die Archimedes (mit dem nach ihm benannten Archimedischen Prinzip) die Grundlagen legte, gehört die Legende des nackt unter „Heureka“ Rufen durch Syrakus rennenden Archimedes:

Der Herrscher von Syrakus hatte den Verdacht, dass ein Goldschmied nicht das ganze ihm übergebene Gold in der bei ihm bestellten Krone verarbeitet hatte, sondern einen Teil abgezweigt und durch eine gewichtsmäßig passende Menge Silbers ersetzt hatte. So wurde Archimedes mit dem Ansinnen konfrontiert, ob er sich eine Methode ausdenken könne, um diesen Verdacht zu überprüfen, ohne dass man die Krone dafür einschmelzen muss. Archimedes soll in der Badewanne gelegen haben, als ihm klar wurde, dass eins der Schlüsselkonzepte seiner Hydrostatik, das Konzept des spezifischen Gewichts, eine Überprüfung des Verdachts ohne Zerstörung der Krone gestattet. Da sprang er nackt wie er war aus der Badewanne und rannte unter Heureka-Rufen zum Palast des Herrschers.

Kommt man auf die rein mathematischen Leistungen von Archimedes zu sprechen, dann ist als Erstes festzuhalten, dass hierzu auch die – nach seinem eigenen Urteil – wertvollste seiner Leistungen, seine Abhandlung zu Kugel und Zylinder, gehört. Eine Arbeit die wir heute eindeutig der Mathematik und nicht der mathematisierten Physik zurechnen. Archimedes seinerseits hat jedoch damals wohl keinen großen Unterschied zwischen diesen beiden wissenschaftlichen Disziplinen gesehen.

Wie dem auch sei: Archimedes war auf seinen durch einen geometrischen Beweis gesicherten Satz, dass jede Kugel ein Volumen von 2/3 des Volumens des umschreibenden Zylinders aufweist, derart stolz, dass er sich ein entsprechendes Relief auf seinem Grabstein wünschte. Durch Cicero wissen wir, dass ihm dieser Wunsch erfüllt wurde.

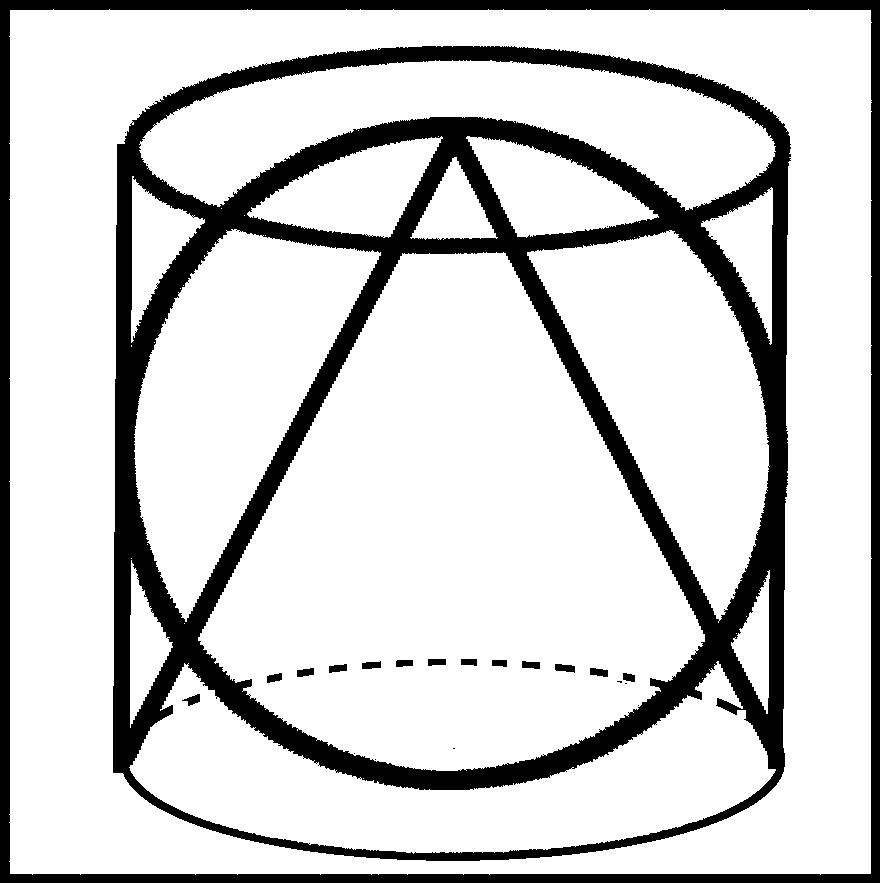
Der von Archimedes bewiesene Satz, dass die Kugel 2/3 des Volumens des umschreibenden Zylinders besitzt, knüpft in mancherlei Weise an den von Eudoxos bewiesenen Satz, dass der Kegel 1/3 des Volumens des umschreibenden Zylinders besitzt an.

Die Volumenverhältnisse der Figuren im Schaubild rechts 1 lauten:

Kegel : Kugel : Zylinder = 1 : 2 : 3

Die Anknüpfung an das Eudoxos Resultat ist dabei nicht nur thematischer Art, sondern sie betrifft auch die Beweistechnik. Archimedes orientiert sich in seinem Beweis an einem bereits von Eudoxos verwendeten Beweisschema:

Man zeigt, dass sowohl die Annahme, dass das Volumen größer als der behauptete Wert ist, zu einem Widerspruch führt,

wie dass auch die Annahme, dass das Volumen kleiner als der behauptete Wert ist, zu einem Widerspruch führt.

Also muss das Volumen genau gleich dem behaupteten Wert sein.

Bei der Herleitung der Widersprüche werden dabei jeweils Verfahren zur geometrischen Näherung der Figuren verwendet.

Im 17. Jahrhundert wurden für diese antike Beweistechnik die etwas unglücklich gewählten Begriffe Exhaustion bzw. Exhaustionsmethode eingeführt.

Archimedes verwendete diese – bis heute meist Exhaustionsmethode genannte – Beweistechnik bereits bei seiner (zeitlich früher anzusetzenden) Beschäftigung mit dem Kreis.

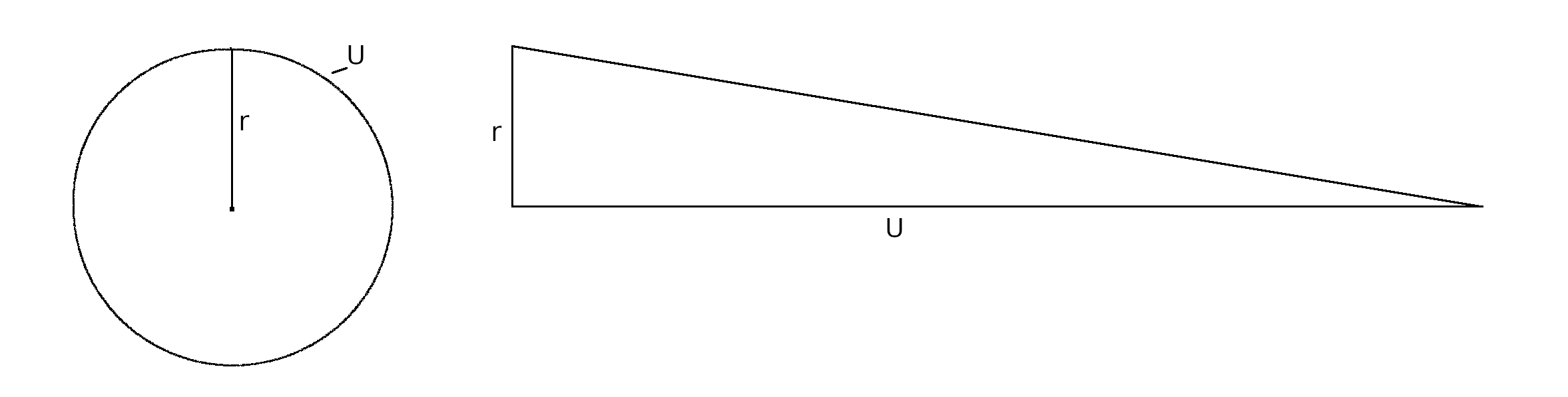
Lange vor der Verfügbarkeit der heute gängigen Formeln für die Fläche von Kreis und Dreieck, beweist er so, dass die Fläche eines Kreises mit den gegebenen Werten Radius r, Umfang U stets der Fläche eines rechtwinkligen Dreiecks mit Katheten der Länge r und U gleich ist (s. Abb.).

Mit Hilfe der nach ihm benannten Archimedischen Spirale zeigte er sogar, wie man solche Flächengleichheiten von Kreis und Dreieck konstruieren kann. Der entscheidende Punkt bei der Konstruktion des zum Kreis flächengleichen Dreiecks ist die Konstruktion einer geraden Linie mit der Länge U. Man spricht da auch gerne von der Rektifikation der Kreislinie.

Ist die Rektifikation der Kreislinie gelungen, so ist es nur noch ein kleiner Schritt zur Quadratur des Kreises. Zur Rektifikation der Kreisline benutzt Archimedes allerdings eine bewegungsgeometrisch definierte Figur: Die Archimedische Spirale. Diese lässt sich nicht allein mit Zirkel und Lineal erzeugen. Dementsprechend bleibt das klassische Problem der Antike, die Konstruktion eines flächengleichen Quadrats zu einem gegebenem Kreis allein mit Zirkel und Lineal (trotz der von Archimedes bewegungsgeometrisch erzeugten Rektifikation der Kreislinie) ungelöst. Es ist in dieser Form jedoch auch nicht lösbar. Es ist also kein Zufall, dass alle Lösungen, die die antiken Griechen zur sogenannten Quadratur des Kreises fanden, stets gegen die Forderung „allein mit Zirkel und Lineal“ verstießen. Wohl weil Archimedes nicht der erste antike Mathematiker war, der eine bewegungsgeometrisch basierte Möglichkeit zur Erzeugung eines einem Kreis flächengleichen Quadrats fand, maß er diesem Aspekt seiner Arbeit keine herausragende Bedeutung bei. Dass es basierend auf seiner Rektifikation der Kreislinie und der dadurch möglichen Konstruktion eines flächengleichen rechtwinkligen Dreiecks, mit den spätestens seit Euklid bekannten Standardverfahren der griechischen Geometrie möglich ist, nun allein mit Zirkel und Lineal vom flächengleichen Dreieck zum flächengleichen Quadrat überzugehen, war ihm in seinem Text zur Archimedischen Spirale (und der dort vorgestellten Rektifikation der Kreislinie) nicht einmal eine ausdrückliche Erwähnung wert.

Dass keine Quadratur des Kreises allein mit Zirkel und Lineal möglich ist, hängt übrigens damit zusammen, dass die für die moderne Kreislehre so zentrale Zahl π (pi) nicht nur eine irrationale sondern sogar eine transzendente Zahl ist. Solche Sachverhalte lagen damals aber selbst für das Jahrtausend-Genie Archimedes weit außerhalb seines Denkhorizontes.

In der Antike bedeutete es schon einen erheblichen Fortschritt, dass Archimedes zeigen konnte, dass

das Verhältnis des Umfangs eines jeden Kreises zu seinem Durchmesser kleiner als 3 1/7 und größer als 3 10/71 ist.

Diese Näherung ist besser als π ≈ 3,14.

Die gründliche Beschäftigung mit der Kreislehre half Archimedes bei der späteren Beschäftigung mit der Kugel. Archimedes nutzte bei seinen Beweisen zu Oberfläche und Volumen der Kugel aus, dass man die Kugel als Rotationskörper des Kreises auffassen kann. So gelang es dem Genie sich von seinen Ergebnissen zu Umfang und Fläche des Kreises einen Weg zu seinen Ergebnissen zu Oberfläche und Volumen der Kugel zu bahnen.

Archimedes ist es auch in etlichen anderen Fällen gelungen, ausgehend von Umfang und Fläche einer ebenen Figur, Oberfläche und Volumen des zugehörigen Rotationskörpers zu bestimmen.

Seine Erfolge bei der Analyse krummlinig begrenzter ebener Figuren und der zugehörigen Rotationskörper lieferten in der Spätrenaissance und frühen Neuzeit eine wichtige Stimulation zur Entwicklung neuer mathematischer Methoden. Man suchte damals nach einem Ansatz, um vergleichbare Resultate erzielen zu können, ohne dafür jeweils anspruchsvolle geometrische Beweise à la Archimedes vorlegen zu müssen. Das Ergebnis dieser wesentlich durch Archimedes inspirierten Bemühungen war die frühe Analysis, die im 17. Jahrhundert, vor allem durch die Arbeiten von Newton und Leibniz, die Mathematik revolutionierte.

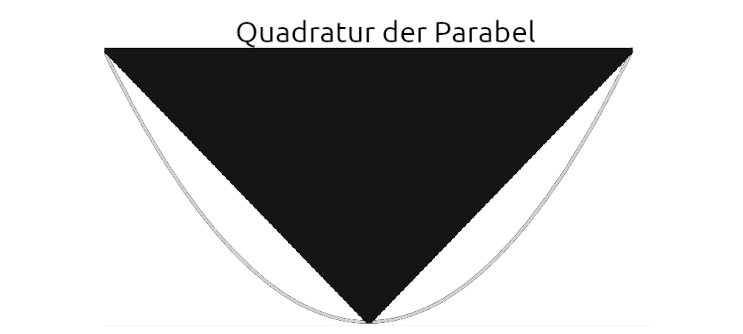
Auch dort, wo Archimedes in seinen Beweisen streng geometrisch argumentiert, nahm er bereits einige der Grundgedanken der Analysis vorweg. Als Musterbeispiel hierfür gilt sein klassisch geometrischer Beweis zur Quadratur des Parabelsegments. In diesem Beweis zeigt Archimedes, dass, wenn man einem Parabelsegment (auf bestimmte Weise) ein Dreieck einbeschreibt, die Fläche des Parabelsegments genau 4/3 dieses einbeschriebenen Dreiecks beträgt.

Von hier aus ist es nur noch ein kurzer Weg bis zur Konstruktion eines zum Parabelsegment flächengleichen Quadrats. Deswegen spricht man von der Quadratur des Parabelsegments, bzw. etwas verkürzt von der Quadratur der Parabel. Erst wenn man zu einer gegebenen, ebenen Figur ein flächengleiches Quadrat konstruieren konnte, galt in der Antike die Frage nach der Fläche der Figur als vollständig beantwortet.

Der von Archimedes vorgelegte Beweis zur Quadratur des Parabelsegments enthält zwar nicht den Begriff des Grenzwerts, kommt aber der zugehörigen mathematischen Denkweise erstaunlich nahe.

Der Analysis noch näher kam Archimedes in seiner sogenannten Mechanischen Methode. Eine entsprechende, heute meist Methodenlehre genannte Schrift des Archimedes wurde im 19. Jahrhundert wiederentdeckt. Sie enthält Argumentationsfiguren, die man problemlos mit den Vorläufern und ersten Anfängen der frühen Analysis in der Spätrenaissance auf eine Stufe stellen kann.

Archimedes verweist in seiner Methodenschrift allerdings ausdrücklich darauf, dass es einigen der dort verwendeten Voraussetzungen an einer zureichenden Begründung ermangelt. Deswegen hat Archimedes von seiner Form der sehr frühen, antiken Analysis in seinen veröffentlichten Beweisen auch keinen Gebrauch gemacht. Er nutzte diese, von ihm als nicht ganz solide eingeschätzte Vorgehensweise jedoch ausgiebig als Hilfsmittel zum Auffinden neuer Sätze und der zugehörigen (klassisch-geometrischen) Beweise.

In Spätrenaissance und früher Neuzeit war man diesbezüglich deutlich weniger zimperlich. Man hat sich von kleineren Unebenheiten bei der Rechtfertigung der Methoden der Analysis nicht groß aufhalten lassen. Archimedes war vom Ideal geometrischer Strenge geprägt und hatte hinsichtlich stringenter Beweise deutlich höhere Ansprüche.

Für jene, die Mathematik lieben, wurden die hier nur angerissenen Themen in einem knapp 70 Seiten umfassenden PDF aufbereitet.

Dieses unter www.antike-griechische.de/Archimedes.pdf verfügbare PDF-Dokument unterliegt einer sehr liberalen Creative Commons Lizenz: http://creativecommons.org/licenses/by-sa/3.0/de/